What Are We Measuring?

When we decide to make a measurement of some quantity in the real world, there are several issues that need to be resolved before we actually make the measurement. Unless these issues are resolved, the measurement will have limited (or no) meaning and quality, and so limited (or no) usefulness.

The first big issue is: Are we quite clear what we are measuring? If the measurement is an ‘indirect’ measurement allowing us to derive an estimate of the quantity we really want, what is the connection between our actual measurement and the value we seek?

Resolving these questions is critical to establishing any kind of repeatability and meaning in the measurement. For example, if we wish to determine the size of a table, what do we mean by its ‘length’?

Is the table perfectly rectangular? The answer must be ‘no,’ because without measurement we cannot tell, and all measurements are imperfect. So how close to rectangular is it? If the two ends are not parallel, we have many different measurements of the distance between the ends, as shown in Figure 1 by dashed lines. (The ‘distortions’ are exaggerated in the figures.)

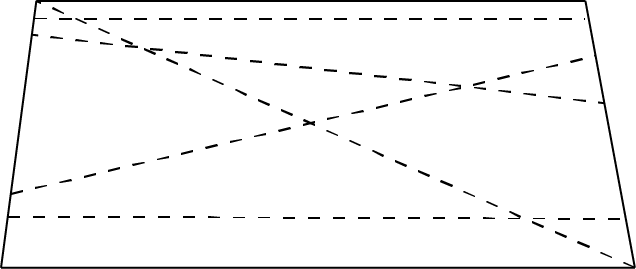
Figure 1

If we measure a quantity several times, we want to have a consistent set of measurements, and the most consistent distance measurement is the minimum or shortest distance. Using Euclidean geometry, the shortest distance between two points, the end points of the measurement, is a straight line. So we make our measurements using straight lines when working with Euclidean geometry. (When working on the surface of the Earth on a large scale, Euclidean geometry does not work properly, as the surface of the planet is a non-Euclidean space. But that is a later, and somewhat more advanced, discussion.)

As shown in Figure 2, non-straight-line distance measurements could take any value above the minimum distance, and so don’t really help reduce the uncertainty in knowing the quantity of interest. They are lower quality measurements, and perhaps could be considered as not being measurements at all in some cases, because they have no impact on that uncertainty.

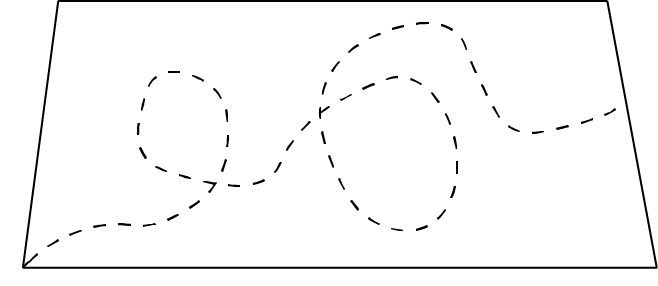
Figure 2

Even with straight lines, we still have multiple possible measurements, and with a table as in Figure 1, the ‘length’ is not well defined. We could say that the measurement had to be perpendicular to one end, but which end, and will that give the shortest distance? We could say that the distance should be measured parallel to one of the other sides, but that, too, has problems, as seen in Figure 3. We cannot determine if the sides are straight, nor even set out a parallel line for the measurement without making additional, imperfect, measurements.

Figure 3

We can resolve the issue of having something definite to measure, as best we can, by measuring between distinct points. With an approximately rectangular table, as shown in Figures 1, 2 and 3, the only distinct points are the corners. This would get complicated for tables with shapes such as shown in Figure 4, as they lack distinct points.

Figure 4

But let us put these particular shapes aside for the moment, and focus on more basic measurement.

If we have a table that is nominally and approximately rectangular, we can designate two distinct points, in this case two of the corners, and measure the straight-line distance between them, as shown in Figure 5.

Figure 5

Now, what are we actually measuring? Is it the true length of the table?

Depending upon the table design, we may not be measuring the actual ‘length.’ We will only be measuring the distance between two corners. Can we use it to represent the length of the table? That depends upon the shape of the table and the purpose of the measurement.

We can make ‘indirect’ measurements of several quantities and then combine them to derive an estimate of the desired quantity. So if we measure the four sides of an approximately rectangular table, as well as the diagonals, using the distinct corners as the points to which measurements are made, as in Figure 6, then we could derive estimates for other quantities.

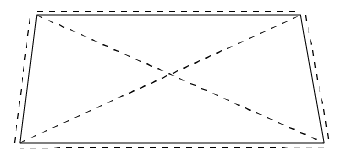
Figure 6

At this point, the purpose of the measurements gets involved. If we can see that the table is reasonably close to rectangle (measuring approximately, ‘by eye’), then we can do simple and approximate measurements if we want to know what size of a tablecloth to buy, or how much paint we would need to paint it. However, if our purpose was to determine the minimum dimensions of a rectangular piece of wood to cover the table (and make it ‘square’), then we would need the more comprehensive measurement set, as shown in Figure 6.

If our purpose was to measure the amount of expansion of the tabletop with changes in room temperature, we would be concerned with making the measurement end points very distinct to facilitate re-measurement.

Pedantry versus Reality

You may think that this is all academic waffling, and that it’s perfectly clear what you are measuring. To a certain extent, you may be right. If we want to measure the table to get the size for a tablecloth, then yes, this is more detail than we need. Everyday measurement doesn’t need all that. And maybe 90% (or more) of measurements are ‘everyday,’ and anybody can make them.

But if we are intending to become measurement experts, there will be times when we really do need to be perfectly clear exactly what we are measuring. Maybe this will be relatively infrequently (for people outside the geospatial discipline), but for expert measurers and those working in the geospatial discipline, this will be the case far more often. It’s the hard and unusual cases where true experts are needed, not the everyday ones.

It’s very easy to measure one thing and think we are learning about something very different. As Richard Feynman pointed out, the first job of a true scientist (and that includes measurement scientists) is to make sure that you aren’t fooling yourself about what you are doing. This must be a very conscious and intentional action, as fooling yourself is very easy to do. Once you have fooled yourself, it is easy to fool others, but there comes a time when someone isn’t fooled and the whole house of cards collapses.

If we measure between the corners of the table we may not be measuring the actual ‘length’ of the table. In cases where the difference matters, we need to know what the difference is. The difference is part of the gap between the reality of measurement (and the object being measured) and the abstraction of the measurement. If we don’t see there is a difference, we have taken the first step to fooling ourselves that there is no gap between abstraction and reality.

Too often, we measure one thing and assume we are making an estimate of some other quantity. We may measure repeat purchases at a store and assume that this is a measure of customer satisfaction. We may measure a vertical location with GPS and assume this is the elevation above our local datum. We may measure the distance between two points in the ground and assume that is the property boundary. But between the measurement and what we think we have estimated, there is the gap.

So before measuring anything, be very clear of the gap between what we want to know (what quantity do we want to estimate) and what we actually measure. This will save a lot of grief later on.